比特币椭圆曲线函数简介与应用

比特币的加密基础是建立在椭圆曲线加密（Elliptic Curve Cryptography，ECC）的数学原理之上。椭圆曲线函数在比特币网络中起着至关重要的作用，它们用于生成公钥、私钥对，以及加密和签名交易。下面我们将对比特币椭圆曲线函数进行简要介绍，并探讨其在加密货币领域的应用。

椭圆曲线函数是一种特殊的数学函数，通常用来描述一个特定形式的曲线，其方程形式为：

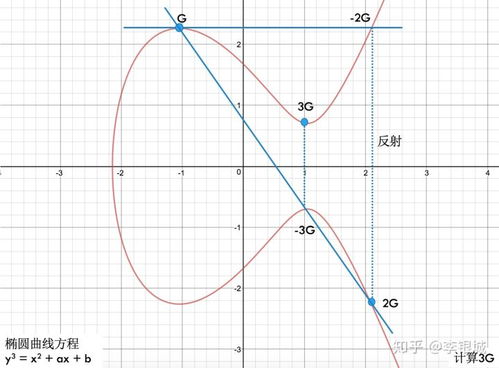
\[y^2 = x^3 ax b\]

其中 \(a\) 和 \(b\) 是常数，且满足特定条件。这些曲线具有许多有趣的性质，包括封闭性、可逆性和离散性。

比特币使用的是一种特定的椭圆曲线函数，称为secp256k1。它的方程为：

\[y^2 = x^3 7\]

其中 \(a = 0\)，\(b = 7\)。这个曲线函数被广泛用于生成比特币地址、公钥和私钥。

比特币椭圆曲线函数在加密货币领域有多种重要应用：

1. 生成公钥和私钥

比特币地址是由公钥通过一系列哈希函数生成的，而公钥则是由私钥通过椭圆曲线函数计算得到的。因此，私钥是生成比特币地址的关键。只要持有私钥，就能够控制与之对应的比特币。

2. 加密和解密

椭圆曲线函数还可用于加密和解密信息。发送者可以使用接收者的公钥对信息进行加密，而只有接收者持有相应的私钥才能解密。

3. 数字签名

比特币交易需要进行数字签名以验证交易的有效性。发送者使用自己的私钥对交易进行签名，而其他人可以使用发送者的公钥验证签名，从而确保交易的真实性和完整性。

尽管椭圆曲线加密在理论上是安全的，但安全性仍然依赖于选择的参数和实现的质量。不安全的曲线参数或不良的实现可能会导致安全漏洞。因此，在设计和实施椭圆曲线加密方案时，需要严格遵循安全最佳实践。

比特币椭圆曲线函数是比特币网络的关键组成部分，它们为生成公钥、私钥对、加密和签名交易提供了数学基础。理解椭圆曲线函数的原理和应用对于深入了解比特币及其他加密货币的工作原理至关重要。

文章已关闭评论！